Итак, вас попросили рассчитать дисперсию с помощью Excel, но вы не знаете, что это значит и как это сделать. Не волнуйтесь, это простая концепция и еще более простой процесс. Вы быстро станете профессионалом в области дисперсии!
Что такое дисперсия?
Дисперсия – это способ измерения среднего расстояния от среднего значения. «Среднее» — это сумма всех значений в наборе данных, деленная на количество значений. Дисперсия дает нам представление о том, имеют ли значения в этом наборе данных тенденцию в среднем равномерно придерживаться среднего значения или разбросаны повсюду.
Математически дисперсия не так уж и сложна:
Как видите, вычислить это значение несложно. Однако, если у вас есть сотни или тысячи значений, вручную это займет целую вечность. Так что хорошо, что Excel может автоматизировать этот процесс!
Для чего вы используете дисперсию?
Вариация сама по себе имеет множество применений. С чисто статистической точки зрения это хороший способ выразить, насколько разбросан набор данных. Инвесторы используют дисперсию для оценки риска тех или иных инвестиций.
Например, взяв стоимость акций за определенный период времени и рассчитав его дисперсию, вы получите хорошее представление о его волатильности в прошлом. Если предположить, что прошлое предсказывает будущее, это будет означать, что что-то с низкой дисперсией является более безопасным и более предсказуемым.
Вы также можете сравнивать отклонения чего-либо в разные периоды времени. Это может помочь обнаружить, когда на что-то влияет другой скрытый фактор, изменяя его дисперсию.
Дисперсия также тесно связана с другой статистикой, известной как стандартное отклонение. Помните, что значения, используемые для расчета дисперсии, возводятся в квадрат. Это означает, что дисперсия не выражается в той же единице, что и исходное значение. Стандартное отклонение требует извлечения квадратного корня из дисперсии, чтобы вернуть значение к исходной единице измерения. Таким образом, если данные были в килограммах, то и стандартное отклонение тоже.
Выбор между генеральной совокупностью и выборочной дисперсией
.В Excel существует два подтипа отклонения с несколько разными формулами. Какой из них выбрать, зависит от ваших данных. Если ваши данные включают всю «население», вам следует использовать дисперсию совокупности. В данном случае «население» означает, что у вас есть все значения для каждого члена целевой группы населения.
Например, если вы посмотрите на вес левшей, то в популяцию входят все левши на Земле. Если вы взвесили их все, вы бы использовали популяционную дисперсию.
Конечно, в реальной жизни мы обычно соглашаемся на меньшую выборку из большей популяции. В этом случае вы должны использовать выборочную дисперсию. Дисперсия населения по-прежнему актуальна для небольших популяций. Например, в компании может быть несколько сотен или несколько тысяч сотрудников, и есть данные о каждом сотруднике. Они представляют собой «население» в статистическом смысле.
Выбор правильной формулы отклонения
В Excel есть три формулы выборочной дисперсии и три формулы генеральной дисперсии:
Вы можете игнорировать VAR и VARP. Они устарели и предназначены только для совместимости с устаревшими электронными таблицами.
Остаются VAR.S и VAR.P, которые предназначены для расчета дисперсии набора числовых значений, а также VARA и VARPA, которые включают текстовые строки.
VARA и VARPA преобразуют любую текстовую строку в числовое значение 0, за исключением «ИСТИНА» и «ЛОЖЬ». Они преобразуются в 1 и 0 соответственно.
Самое большое отличие состоит в том, что VAR.S и VAR.P пропускают любые нечисловые значения. При этом эти случаи исключаются из общего числа значений. Это значит, что среднее значение будет другим, поскольку для получения среднего значения нужно разделить на меньшее количество случаев.
Как рассчитать дисперсию в Excel
Все, что вам нужно для расчета дисперсии в Excel, — это набор значений. В приведенном ниже примере мы собираемся использовать VAR.S, но формула и методы будут одинаковыми независимо от того, какую формулу отклонения вы используете:
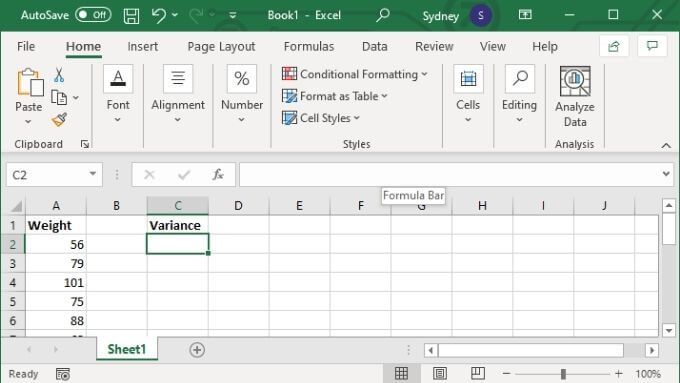<старый старт="2">
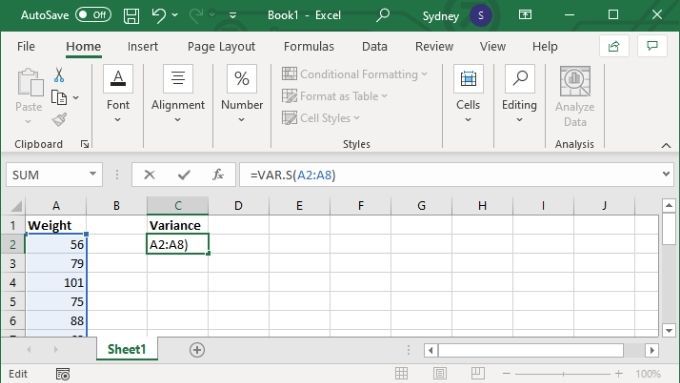
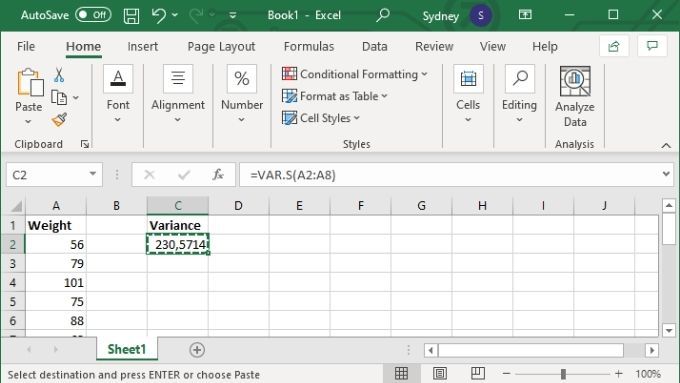
Кроме того, вы можете указать конкретные значения, и в этом случае формула будет выглядеть так: =VAR.S(1,2,3,4) . Числа заменены на все, что вам нужно для расчета дисперсии. Таким образом, вы можете ввести до 254 значений вручную, но если у вас всего несколько значений, почти всегда лучше ввести данные в диапазон ячеек, а затем использовать версию формулы для диапазона ячеек, описанную выше.
Вы можете преуспеть в Excel
Вычисление дисперсии — полезный прием для всех, кому нужно выполнить некоторую статистическую работу в Excel. Но если какая-либо терминология Excel, которую мы использовали в этой статье, вас сбивает с толку, рассмотрите возможность использования Учебное пособие по основам Microsoft Excel – обучение использованию Excel.
Если же вы готовы к большему, воспользуйтесь Добавьте линию тренда линейной регрессии в диаграмму рассеяния Excel, чтобы визуализировать дисперсию или любой другой аспект вашего набора данных по отношению к среднему арифметическому.
>.